O Quadrado Mágico de Dirichlet

Johann Peter Gustav Lejeune Dirichlet foi um matemático alemão - 13 de fevereiro de 1805 - 5 de maio de 1859 que fez profundas contribuições à teoria dos números. Criou, inclusive o campo de Teoria Analítica de Números, e à teoria da Série de Fourier e outros tópicos em mathematical analysis. Ele tem o crédito de ser o primeiro matemático a dar uma definição formal moderna do que é uma função.

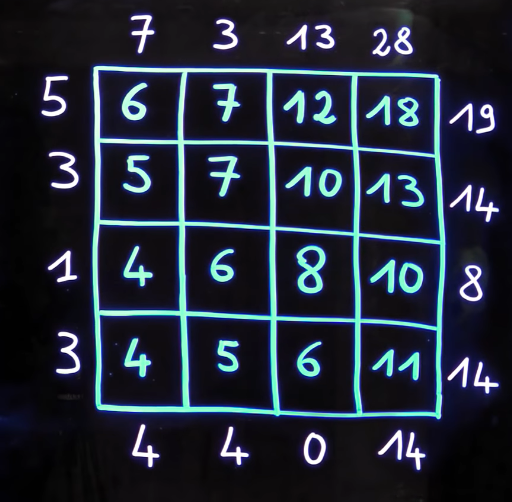
Os quadrados mágicos de Dirichlet são bem descritos nas apresentações de Olivier Druet. Seu primeiro exemplo é mostrada à esquerda. Ele consiste de uma matriz rodeada por números aleatórios cujos números interiores são iguais a média aritimética dos seus vizinhos. Assim, se são dados os números exteriores da matriz, o primeiro elemento da matriz, por exemplo, é a média aritimética de (5 + 7 + 7 + 5)/4 = 6. O terceiro elemento diagonal, 8 = ( 6 + 10 + 10 + 6)/4 etc.

O problema consiste em: Dados os elementos exteriores, como determinar todos os elementos interiores

Para verificar uma prova do método, por favor, entre uma dimensão desejada da matriz (por favor não exagere):

Primeira tentativa

A primeira tentativa consistiria em escrever as equações para todas as definições, considerando uma matriz A com n×n elementos. Para o exemplo acima, temos que resolver uma matrix de 4×4, de forma que a matriz de trabalho seria de 6×6, n = 6.
a₀₀ a₀₁ a₀₂ . . . a_0n
a₁₀ a₁₁ a₁₂ . . . a_1n
. . .
a_n0 a_n1 a_n2 . . . a_nn

Para o exemplo acima vemos que podemos construir 16 equações lineares de primeira ordem com 16 colunas. Assim, para o exemplo, nós teríamos

a₁₁ = (a₁₀ + a₀₁ + a₁₂ + a₂₁)/4 ou -4a₁₁ + a₁₂ + a₂₁ = -(a₀₁ + a₁₀) ( 1)
a₁₂ = (a₁₁ + a₀₂ + a₁₃ + a₂₂)/4 ou a₁₁ - 4a₁₂ + a₁₃ + a₂₂ = -a₀₂ ( 2)
a₁₃ = (a₁₂ + a₀₃ + a₁₄ + a₂₃)/4 ou a₁₂ - 4a₁₃+ a₁₄ + a₂₃ = -a₀₃ ( 3)
a₁₄ = (a₁₃ + a₀₄ + a₁₅ + a₂₄)/4 ou a₁₃ + a₁₅ - 4a₁₄+ a₂₄ = -a₀₄ ( 4)
. . . . . . . . . .
a₄₄ = (a₄₃ + a₃₄ + a₄₅ + a₅₄)/4 ou a₄₃ + a₃₄ - 4a₄₄ = -(a₄₅ + a5) (16)

Isto pode ser representado como um sistema de equações lineares da forma
| A | × | x | = | k |, cuja solução é
| x | = | A |^-1 × | k |.
Isto é, os valores internos são vetores resultantes da multiplicação da matriz inversa de A com as constantes externas.

0		11	12	13	14	21	22	23	24	31	32	33	34	41	42	43	44
	|	-4	1	0	0	1	0	0	0	0	0	0	0	0	0	0	0 |		| a11 |		|	-a01 - a10	|
	|	1	-4	1	0	0	1	0	0	0	0	0	0	0	0	0	0 |		| a12 |		|	-a02	|
	|	0	1	-4	1	0	0	1	0	0	0	0	0	0	0	0	0 |		| a13 |		|	-a03	|
	|	0	0	1	-4	0	0	0	1	0	0	0	0	0	0	0	0 |		| a14 |		|	-a04 - a15	|
	|	1	0	0	0	-4	1	0	0	1	0	0	0	0	0	0	0 |		| a21 |		|	-a20	|
	|	0	1	0	0	1	-4	1	0	0	1	0	0	0	0	0	0 |		| a22 |		|	0	|
	|	0	0	1	0	0	1	-4	1	0	0	1	0	0	0	0	0 |		| a23 |		|	0	|
	|	0	0	0	1	0	0	1	-4	0	0	0	1	0	0	0	0 |		| a24 |		|	-a25	|
	|	0	0	0	0	1	0	0	0	-4	1	0	0	1	0	0	0 |	x	| a31 |	=	|	-a30	|
	|	0	0	0	0	0	1	0	0	1	-4	1	0	0	1	0	0 |		| a32 |		|	0	|
	|	0	0	0	0	0	0	1	0	0	1	-4	1	0	0	1	0 |		| a33 |		|	0	|
	|	0	0	0	0	0	0	0	1	0	0	1	-4	0	0	0	1 |		| a34 |		|	-a35	|
	|	0	0	0	0	0	0	0	0	1	0	0	1	-4	1	0	0 |		| a41 |		|	-a40 - a51	|
	|	0	0	0	0	0	0	0	0	0	1	0	0	1	-4	1	0 |		| a42 |		|	-a52	|
	|	0	0	0	0	0	0	0	0	0	0	1	0	0	1	-4	1 |		| a43 |		|	-a53	|
	|	0	0	0	0	0	0	0	0	0	0	0	1	0	0	1	-4 |		| a44 |		|	-a45 - a54	|

Note que a₀₀, a_0n, a_n0, a_nn não são usados e a_0x, a_x0 e a_xn são constantes dadas. Assim, temos que resolver (n-2) equações com (n-2) variáveis. Então, se uma matriz A tem uma inversa, existe uma solução para o quadrado mágico de Dirichlet. Note também que A aparenta ser uma matriz esparsa, de forma que o seu processo de inversão deve ser rápído, sabendo escolher o algorítimo de inversão apropriado.

Valores para o exemplo de Druet são mostrados abaixo. Estas matrizes pode ser selecionadas, copiadas e coladas em qualquer resolvedor de equações lineares disponíveis na internet para encontrar o resultado. Por exemplo, você pode usar BlueBit - Linear Equations Solver.

Segunda tentativa

Outra solução, mais adequada e simples já que inversão de matrizes pode ser desgastante em programação de computadores é resolver as equações por aproximação sucessiva. Se lembrarmos que zero é a média aritimética se todos seus termos são nulos e que a média é sempre menor que o menor número que a compõe, não importando se usamos números negativos, inteiros, reais, etc, Podemos começar preenchendo a matriz com zeros, calculando a média de cada um, substituindo cada um deles e continuando a calcular até que a variação entre dois valores calculados seja menor que um valor de erro previamente escolhido. Assim, podemos calcular até atingirmos o número de casas decimais com a precisão selecionada que nos agrade. Você pode também limpar a matriz com um click sobre "Limpar matriz".

Você pode mudar os valores externos da matriz. Caso contrário, os números externos são gerados aleatoriamente entre -100 a +100. Você pode alterar a precisão de cálculo alterando o valor do "Erro máximo". Não é aconselhável utilizar matrizes com dimensões muito altas (acimade 20). É interessantes também notar que o número de iterações necessárias para conseguir uma solução adequada raramente é grande. Você poderá, por favor, gerar uma matriz quadrada 4x4 aleatória, inserir os dados de Olivier do exemplo acima e executar uma tentativa. O número máximo de iterações deste serviço foi limitado a 10.000. Esperamos que você não chegue a tanto. Aproveite.