
Johann Peter Gustav Lejeune Dirichlet was a german mathematician - 13 February 1805 – 5 May 1859 who made deep contributions to number theory (including creating the field of analytic number theory), and to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a function.
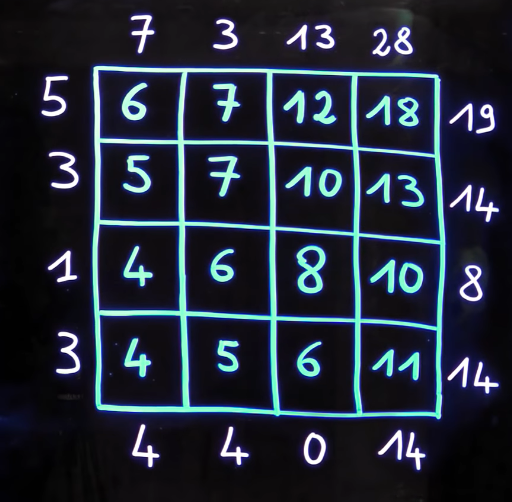
Dirichlet magic squares are very well described in Olivier Druet´s presentation. His first example is shown to the left. It consists of an array surrounded by random numbers whose interior numbers are equal to the arithmetic mean of its neighbors. So given the outside numbers, the first element of the array, for example, "6" is the arithmetic mean of (5 + 7 + 7 + 5)/4. Third diagonal element, 8 = ( 6 + 10 + 10 + 6)/4 etc.
The problem consists in, given the exterior elements, how to determine all interior elements.
To taste the method, please enter the magic square dimension:
and
First try
Firts try would be to write the equations for all definitions, considering an array A with n×n elements.
For the example above, we have to solve an array 4×4, so the working array would be 6×6, n = 6.
a00 a01 a02 . . . a0n
a10 a11 a12 . . . a1n
. . .
an0 an1 an2 . . . ann
For the example above we see that we can construct 16 first order linear equations with 16 unkowns.
a11 = (a10 + a01 + a12 + a21)/4
or
-4a11 + a12 + a21 = -(a01 + a10)
( 1)
a12 = (a11 + a02 + a13 + a22)/4
or
a11 - 4a12 + a13 + a22 = -a02
( 2)
a13 = (a12 + a03 + a14 + a23)/4
or
a12 - 4a13+ a14 + a23 = -a03
( 3)
a14 = (a13 + a04 + a15 + a24)/4
or
a13 + a15 - 4a14+ a24 = -a04
( 4)
. . . . . . . . . .
a44 = (a43 + a34 + a45 + a54)/4
or
a43 + a34 - 4a44 = -(a45 + a5)
(16)
This can be represented as a linear equations systems of the form
| A | × | x | = | k |, which can be solved as
| x | = | A |-1 × | k |.
That is, the internal square values is a vector resulting from the matrix multiplication
of the inverse of | A | to the external given constants.
| 0 | 11 | 12 | 13 | 14 | 21 | 22 | 23 | 24 | 31 | 32 | 33 | 34 | 41 | 42 | 43 | 44 | |||||||
| | | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | | a11 | | | | -a01 - a10 | | | |||
| | | 1 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | | a12 | | | | -a02 | | | |||
| | | 0 | 1 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | | a13 | | | | -a03 | | | |||
| | | 0 | 0 | 1 | -4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | | a14 | | | | -a04 - a15 | | | |||
| | | 1 | 0 | 0 | 0 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | | | a21 | | | | -a20 | | | |||
| | | 0 | 1 | 0 | 0 | 1 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | | | a22 | | | | 0 | | | |||
| | | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | | | a23 | | | | 0 | | | |||
| | | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | | | a24 | | | | -a25 | | | |||
| | | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | | x | | a31 | | = | | | -a30 | | | |
| | | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 1 | 0 | 0 | 1 | 0 | 0 | | | a32 | | | | 0 | | | |||
| | | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 1 | 0 | 0 | 1 | 0 | | | a33 | | | | 0 | | | |||
| | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 0 | 0 | 0 | 1 | | | a34 | | | | -a35 | | | |||
| | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 1 | 0 | 0 | | | a41 | | | | -a40 - a51 | | | |||
| | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 1 | 0 | | | a42 | | | | -a52 | | | |||
| | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | 1 | | | a43 | | | | -a53 | | | |||
| | | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | -4 | | | a44 | | | | -a45 - a54 | | |
It should be noted that a00, a0n, an0, ann are not used and a0x, ax0 and axn are given constants. So, we have to solve (n-2) equations with n-2 variables. So, if matrix A has an inverse a solution exists for Dirichlet magic square. It is also to be noted that A seams sparse, so the inverse process should be fast with the appropriate algorithm.
Values for Druet's example is show below. These matrices may be selected, copied a pasted in any on-line free linear system equations solver available in the internet to verify the result. You may use, for example, BlueBit - Linear Equations Solver.
Second try
Another solution, more adequate and easy than inverting matrices in computer programming is to solve by successive approximation. If we remember that zero is the arithmetic mean if all terms that compose it are zero and that the mean is always smaller than the smallest of the numbers that compose it, no matter if we use positive or negative numbers of if we use integers of real numbers, we can start filling the interior matrix or array with zeros, calculate the mean for each one, substitute each of them and continue to calculate until the variation of the calculated values is smaller than a chosen error. So we can iterate until we get the decimal places precision that pleases us.
You can change data from the surroundings of the matrix. Surrounding numbers are randomly generated
between -100 to +100. You can choose to reinit the result by clicking on "Clear Matrix"
and also modify the maximum error to gain insight on calculation behavior and precision. It is not
advisable to use too large matrix dimensions (above 20). It is notable, finally, that the number of
iterations before a graceful termination is rarely large. You may please, generate a 4 x 4 square
matrix, insert Olivier´s data from the above example and give it try. The maximum number of
iterations is limited to 10,000. We hope you don´t get there. Enjoy.

